Skip to content

ray-tracing 光线追踪基本原理

· 17 min
TL;DR

详细解析轻量级光线追踪引擎的实现原理，从视口构建到透视投影的完整过程

本文详细介绍光线追踪的基本原理和实现方法，以直观的方式解释光线如何与物体相交并生成图像。文章从 PPM 格式图像表示开始，深入讲解射线数学表达、点乘与叉乘等向量运算的几何意义，并展示了主射线、阴影射线、反射射线和折射射线如何协同工作构建逼真的 3D 渲染场景。

首先理解这三件事：

  1. 人的眼睛能看到东西，是因为光从物体上反射进入到人眼，根据光线可逆性，我们可以把这个过程”想象”是由于人的眼睛发出光，投射到物体上，于是物体被看见了。现在，基于这个概念，用一条直线，带有方向，来模拟人眼，就称为 ray 线吧，即射线。

  2. 数学知识：平面有两个点：O 点，P 点，O 点固定，P 点运动，但是 P 点的运动受到约束：(Px−Ox)2+(Py−Oy)2=r2(P_x-O_x)^2 + (P_y-O_y)^2 = r^2 那么 P 点的运动轨迹肯定是一个平面圆。三维的立体圆也一样。

  3. 如果 ray 向空间任意方向发射光线，再假设存在一个完全透明的立体球（此时完全看不见），当 ray 线与它相交 (交点为 1，在表面，交点为 2，穿过内部)，这个时候将交点以及交点内部都涂色，是不是马上就能看见这个立体球了？只需要满足约束：(Px−Ox)2+(Py−Oy)2+(Pz−Oz)2=r2(P_x-O_x)^2 + (P_y-O_y)^2 + (P_z-O_z)^2 = r^2 即可。这其实就渲染出来了一个 3D 的球体。

好了，理解了这个就理解了光线追踪最基本的知识，然后你就能画出如下的图了：

image.png

基础#

先从最基本的来，打好基础，把框架做好。以下都是基于三维坐标进行构建的。

1. 如何表示图片？#

这里使用 PPM 图片格式，其最简单的内容如下：

P3
# 注释
3 2
255
255   0   0     0 255   0     0   0 255
255 255   0   255 255 255     0   0   0

所以实际图片显示如下：

img

2. 数学基础#

射线 前面提到的 ray 射线，在空间中满足： P(t)=A+tb\mathbf{P}(t) = \mathbf{A} + t\mathbf{b}

其中:

如果要展示具体的分量形式，可以写作：

[AxAyAz]+t[bxbybz]\begin{bmatrix} A_x \\ A_y \\ A_z \end{bmatrix} + t\begin{bmatrix} b_x \\ b_y \\ b_z \end{bmatrix}

涉及到向量以及矩阵，但是不需要深究，代码实现起来也不难理解。现在只需要明白几个知识点即可。

射线又可以分为：

  1. 视线射线 (View Ray):

又叫做主射线，主射线是从相机/观察点 (view point) 发出，穿过图像平面上的每个像素，用于确定该像素”看到”的场景内容。这些射线决定了哪些物体会出现在最终渲染的图像中。

  1. 阴影射线 (Shadow Ray)
相机 光源 交点 阴影射线 反射射线 折射射线

阴影射线又叫次级射线，它是从物体表面的交点发出，用于计算光照、阴影、反射和折射等效果。主要包括：

点乘

向量 a 和 b 的点乘 (dot)，表示如下： a⋅b=axbx+ayby+azbz=∣a∣∣b∣cos⁡θ\mathbf{a} \cdot \mathbf{b} = a_x b_x + a_y b_y + a_z b_z = |\mathbf{a}||\mathbf{b}|\cos\theta

对应的矩阵表达方式是： a⋅b=[axayaz][bxbybz]\mathbf{a} \cdot \mathbf{b} = \begin{bmatrix} a_x & a_y & a_z \end{bmatrix} \begin{bmatrix} b_x \\ b_y \\ b_z \end{bmatrix}

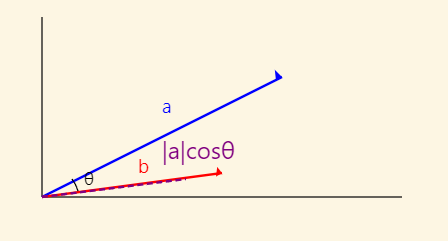
image.png

*点乘的几何意义：

叉乘

对于向量 a\mathbf{a} 和 b\mathbf{b}，叉乘 (cross) 可以表示为：

a×b=∣ijkaxayazbxbybz∣\mathbf{a} \times \mathbf{b} = \left| \begin{matrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ a_{x} & a_{y} & a_{z} \\ b_{x} & b_{y} & b_{z} \end{matrix} \right|

展开后得到：

a×b=(aybz−azbyazbx−axbzaxby−aybx)\mathbf{a} \times \mathbf{b} = \begin{pmatrix} a_{y} b_{z} - a_{z} b_{y} \\ a_{z} b_{x} - a_{x} b_{z} \\ a_{x} b_{y} - a_{y} b_{x} \end{pmatrix}

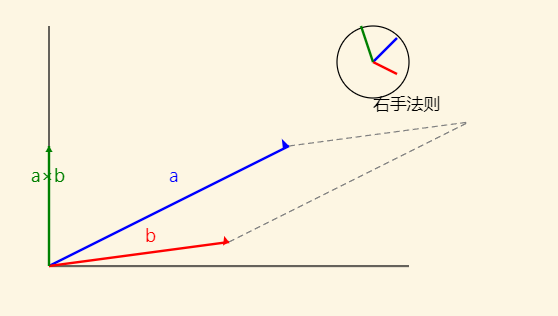
image.png

叉乘的几何意义：

  1. 结果是一个向量，且垂直于 a\mathbf{a} 和 b\mathbf{b}
  2. 方向遵循右手定则
  3. 模长等于 ∣a∣∣b∣sin⁡θ|\mathbf{a}||\mathbf{b}|\sin\theta
  4. 等于由两向量构成的平行四边形的面积
  5. 常用于计算法向量

用代码表示如下：

// 省略其他代码


using point3 = vec3;


// 点乘
inline double dot(const vec3& u, const vec3& v) {
    return u.e[0] * v.e[0]
        + u.e[1] * v.e[1]
        + u.e[2] * v.e[2];
}


// 叉乘
inline vec3 cross(const vec3& u, const vec3& v) {
    return vec3(
        u.e[1] * v.e[2] - u.e[2] * v.e[1],
        u.e[2] * v.e[0] - u.e[0] * v.e[2],
        u.e[0] * v.e[1] - u.e[1] * v.e[0]
    );
}
// 单位向量
inline vec3 unit_vector(const vec3& v) {
    return v / v.length();
}

ray 射线的表达：

#ifndef RAY_H
#define RAY_H


#include "vec3.h"
class ray {
  public:
    // ray 的构造函数
    ray() {}
    ray(const point3& origin, const vec3& direction) : orig(origin), dir(direction) {}


    // 原点以及方向
    const point3& origin() const  { return orig; }
    const vec3& direction() const { return dir; }
    // 当前的位置表达：p_at = orig + t*dir
    point3 at(double t) const {
        return orig + t*dir;
    }


  private:
    point3 orig;
    vec3 dir;
};


#endif

3. 空间坐标#

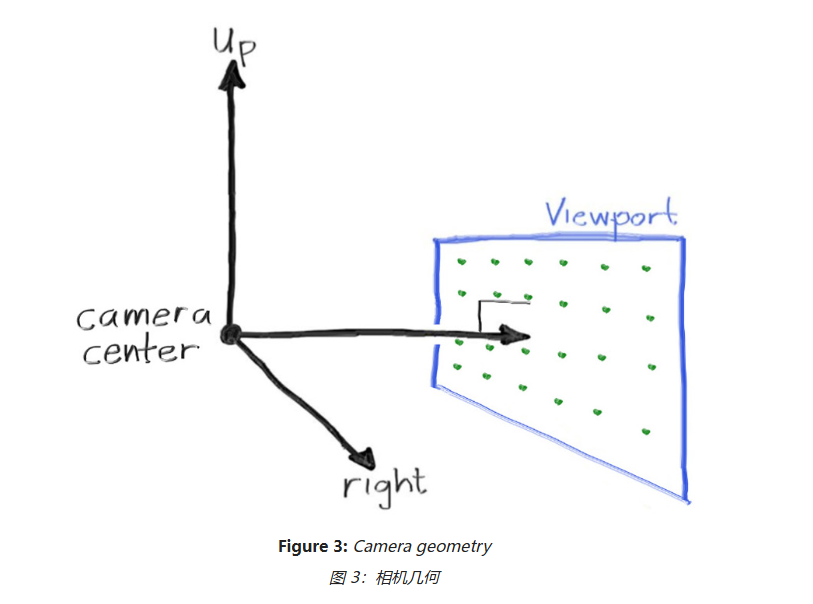
现在假设有一个相机，它是射线的出发点，作为原点，坐标是 (0,0,0)。然后还需要一个屏幕，这里我们叫做 viewport , 但是它也是虚拟的，是由像素矩阵组成的，对应着我们能看到的图像的平面。它们目前的关系如下： image.png

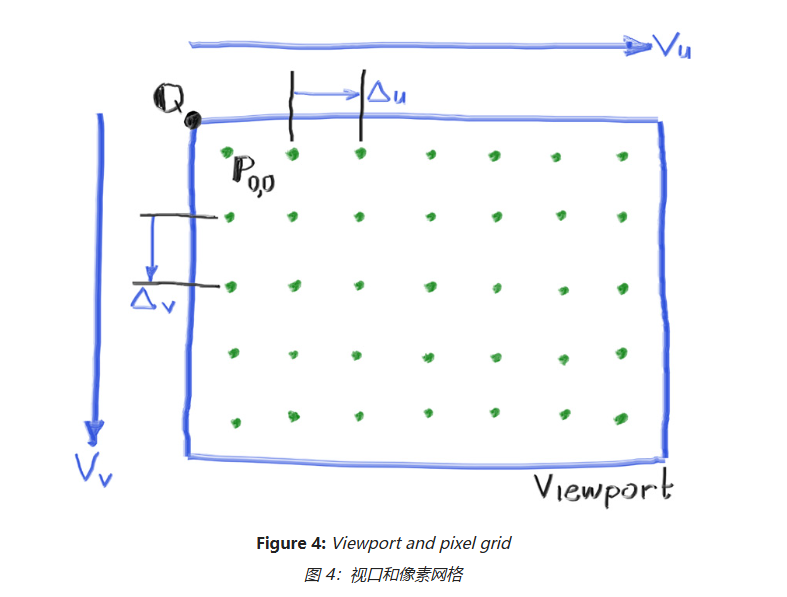
回到像素矩阵平面，其坐标如下： image.png

这里要区分视口原点 Q，像素原点 P(0,0)，它们的坐标是不一样的。

现在使用代码来实现这些坐标，如下：

    auto aspect_ratio = 16.0 / 9.0;  // 设置长宽比，可调整
    int image_width = 400;           // 图像宽度


    // 根据图像宽度，计算图像高度
    int image_height = int(image_width / aspect_ratio);
    image_height = (image_height < 1) ? 1 : image_height;


    // 相机
    // 相机原点到视口中心点的垂直距离
    auto focal_length = 1.0;
    // viewport 的 高度
    auto viewport_height = 2.0;
    // 根据 viewport 的高度，计算其宽度
    auto viewport_width = viewport_height * (double(image_width)/image_height);
    // 相机中心点
    auto camera_center = point3(0, 0, 0);


    // viewport 的 U，V 方向坐标
    auto viewport_u = vec3(viewport_width, 0, 0);
    auto viewport_v = vec3(0, -viewport_height, 0);


    // Calculate the horizontal and vertical delta vectors from pixel to pixel.
    // viewport 上面的像素点间的距离 (u，v 方向根据 viewport 的宽和高来分别计算)
    auto pixel_delta_u = viewport_u / image_width;
    auto pixel_delta_v = viewport_v / image_height;


    // Calculate the location of the upper left pixel.
    // 计算得到左上角 Q 点的坐标
    auto viewport_upper_left = camera_center
                             - vec3(0, 0, focal_length) - viewport_u/2 - viewport_v/2;
    // 计算得到起始像素点的坐标 (P(0,0) 点)
    auto pixel00_loc = viewport_upper_left + 0.5 * (pixel_delta_u + pixel_delta_v);

有了相机中心点，viewport 的左上角的点，和像素的第一个点 (扫描所有像素点时，从左到右，从上到下，因此左上角是起点)

    // 按行从左到右扫描
    for (int j = 0; j < image_height; j++) {
        // 从上到下扫描列
        for (int i = 0; i < image_width; i++) {
            // 每次扫描时的像素点坐标
            auto pixel_center = pixel00_loc + (i * pixel_delta_u) + (j * pixel_delta_v);
            // ray 射线方向，由相机中心点指向像素点
            auto ray_direction = pixel_center - camera_center;
            // 因此获得 ray 射线
            ray r(camera_center, ray_direction);
            // 射线所扫描到的点，使用 ray_color 进行着色
            color pixel_color = ray_color(r);
            // 着色后，写入图像
            write_color(std::cout, pixel_color);
        }
    }


color ray_color(const ray& r) {
    return color(0,0,0);
}

4. 渲染#

前面已经完成部分代码，以下是主代码:

#include "color.h"
#include "ray.h"
#include "vec3.h"
#include <iostream>


color ray_color(const ray& r) {
    return color(0,0,0);
}


int main() {


    // Image
    auto aspect_ratio = 16.0 / 9.0;
    int image_width = 400;


    int image_height = int(image_width / aspect_ratio);
    image_height = (image_height < 1) ? 1 : image_height;


    // Camera
    auto focal_length = 1.0;
    auto viewport_height = 2.0;
    auto viewport_width = viewport_height * (double(image_width)/image_height);
    auto camera_center = point3(0, 0, 0);


    auto viewport_u = vec3(viewport_width, 0, 0);
    auto viewport_v = vec3(0, -viewport_height, 0);


    auto pixel_delta_u = viewport_u / image_width;
    auto pixel_delta_v = viewport_v / image_height;


    auto viewport_upper_left = camera_center
                             - vec3(0, 0, focal_length) - viewport_u/2 - viewport_v/2;
    auto pixel00_loc = viewport_upper_left + 0.5 * (pixel_delta_u + pixel_delta_v);


    // Render
    std::cout << "P3\n" << image_width << " " << image_height << "\n255\n";


    for (int j = 0; j < image_height; j++) {
        std::clog << "\rScanlines remaining: " << (image_height - j) << ' ' << std::flush;
        for (int i = 0; i < image_width; i++) {
            auto pixel_center = pixel00_loc + (i * pixel_delta_u) + (j * pixel_delta_v);
            auto ray_direction = pixel_center - camera_center;
            ray r(camera_center, ray_direction);


            color pixel_color = ray_color(r);
            write_color(std::cout, pixel_color);
        }
    }


    std::clog << "\rDone.                 \n";
}

渲染的关键部分在于，获得 ray 射线后：

  // 获得 ray 射线
  ray r(camera_center, ray_direction);
  // 对射线所指向的点进行着色，即渲染
  color pixel_color = ray_color(r);
  // 着色后写入图像文件
  write_color(std::cout, pixel_color);


color ray_color(const ray& r) {
    //目前 渲染的点都为 (0,0,0) 即为黑色
    return color(0,0,0);
}

结果如下： image.png

为了渲染其他颜色，需要更改 ray_color 的逻辑。这里我们想先做一个简单的渐变效果。

有一种方法叫做线性混合 或 线性插值： f(a)=(1−a)⋅v0+a⋅v1f(a) = (1-a) \cdot v_0 + a \cdot v_1 其图像是：

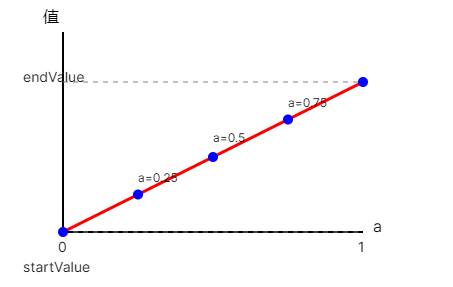
应用到代码中是这样：

color ray_color(const ray& r) {
    vec3 unit_direction = unit_vector(r.direction());
    auto a = 0.5*(unit_direction.y() + 1.0);
    return (1.0-a)*color(1.0, 1.0, 1.0) + a*color(0.5, 0.7, 1.0);
}

所有图片变成渐变了： image.png

5. 渲染球体#

根据前面的数学知识，我们已经知道了绘制一个想象中的球体是如何了。假设我们要在 viewport 中心处渲染处这个球体，目前球的中心点已知，ray 射线也已知，那么只剩下解方程了: P(t)=A+tb\mathbf{P}(t) = \mathbf{A} + t\mathbf{b} (Cx−x)2+(Cy−y)2+(Cz−z)2=r2(C_x - x)^2 + (C_y - y)^2 + (C_z - z)^2 = r^2

P=(x,y,z) 到中心 C=(Cx,Cy,Cz) 的向量是 (C−P), 那么球的表面方程为：(C−P)⋅(C−P)=r2

求球根公式是： x=−b±b2−4ac2ax = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} ，当它无解时，表明 ray 射线与其不相交，当存在一个根时，表示想切，存在两个根，表示相交并穿过 (不过这在现在的场景下与一个根区别不大)。

// 判断 ray 射线是否碰撞到球体
bool hit_sphere(const point3& center, double radius, const ray& r) {
    // C-Q
    vec3 oc = center - r.origin();


    // 简化后的求根公式的系数分解
    auto a = dot(r.direction(), r.direction());
    auto b = -2.0 * dot(r.direction(), oc);
    auto c = dot(oc, oc) - radius*radius;


    // 判断 b2 - 4ac 的大小
    auto discriminant = b*b - 4*a*c;
    大于或等于 0 时，说明有根，因此射线 ray 与球体相交。
    return (discriminant >= 0);
}


color ray_color(const ray& r) {
    // 球体的中心点为 (0,0,-1), 即在 Z 轴方向上距相机原点 (0,0,0) 1 个单位距离。半径 0.5，
    if (hit_sphere(point3(0,0,-1), 0.5, r))
      // 当与球体相交时，渲染为红色
        return color(1, 0, 0);
    // 其余情况，保持渐变
    vec3 unit_direction = unit_vector(r.direction());
    auto a = 0.5*(unit_direction.y() + 1.0);
    return (1.0-a)*color(1.0, 1.0, 1.0) + a*color(0.5, 0.7, 1.0);
}

image.png

结果如预期一样，渲染出了一个球体，从想象中透明的球体变为可见的了。

6. 球体表面法线着色#

球体表面的法线即为垂直于表面的一条线，在坐标系中它位于从球心指向表面交点的方向。

刚才我们使用 ray 射线进行着色，现在使用球体表面法线进行着色。

代码如下：

double hit_sphere(const point3& center, double radius, const ray& r) {
    vec3 oc = center - r.origin();
    auto a = dot(r.direction(), r.direction());
    auto b = -2.0 * dot(r.direction(), oc);
    auto c = dot(oc, oc) - radius*radius;
    auto discriminant = b*b - 4*a*c;


    if (discriminant < 0) {
        return -1.0;
    } else {
      // 求最小根，即离相机原点最近的交点。
        return (-b - std::sqrt(discriminant) ) / (2.0*a);
    }
}


color ray_color(const ray& r) {
    auto t = hit_sphere(point3(0,0,-1), 0.5, r);
    if (t > 0.0) {
        // 当存在最小根时，计算法线，并将之转换为单位向量。t.at(t) 即为球体表面交点
        vec3 N = unit_vector(r.at(t) - vec3(0,0,-1));
        // 将法线每个分量的范围缩放到 [0,1]  （N.x() 最大是 1 个单位）
        // 这也产生一种平滑的渐变效果
        return 0.5*color(N.x()+1, N.y()+1, N.z()+1);
    }


    vec3 unit_direction = unit_vector(r.direction());
    auto a = 0.5*(unit_direction.y() + 1.0);
    return (1.0-a)*color(1.0, 1.0, 1.0) + a*color(0.5, 0.7, 1.0);
}

于是球体也有了渐变色： image.png

用下面的示意图总结一下整个渲染流程的核心步骤：

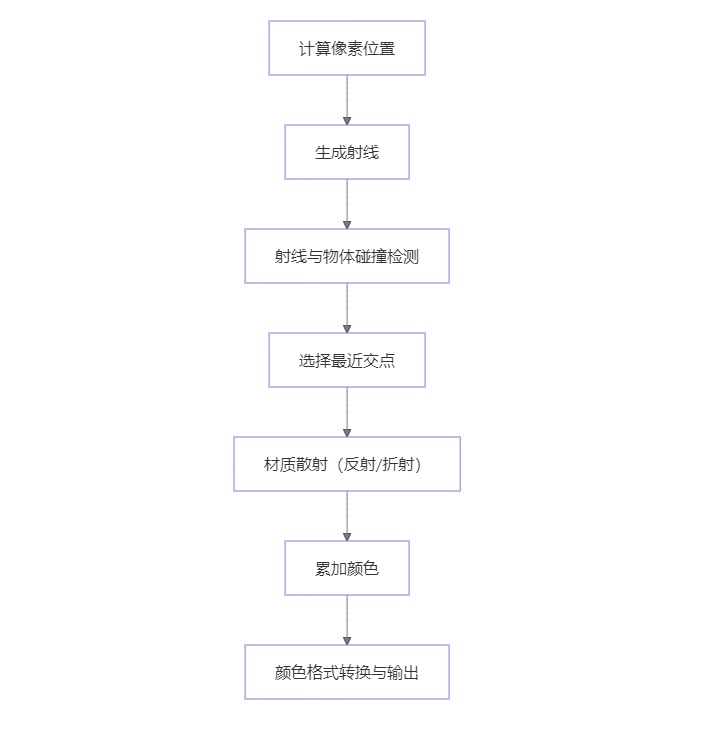
后续#

后面还有对交点附近的点进行抗锯齿处理、表面漫反射处理、折射处理，以及根据不同材料表面的反射情况做不同的处理等等更复杂的处理，时间有限，这样就先不写了，后面有时间再继续写。有兴趣可以看参考链接。

参考链接：#

  1. https://raytracing.github.io/books/RayTracingInOneWeekend.html